SRM 669 Div1 Easy 250 SubdividedSlimes

問題概要

サイズSのスライムが与えられる。
以下の行動を繰り返す。
1:2以上のサイズsのスライムに注目する。
2:s=x+yとなるようにスライムをサイズxとyに分割する。(x > 0, y > 0)
3:得点としてx*yを得る。
4:1に戻る。
得点M以上を得るためには最小で何回スライムを分ければいいか

解法

嘘解法っぽいけど通ったので正義。

スライムは最大でS-1回しか分割することができないので、
t回の分割でどれだけ得点を最大化できるかを考える。

t = 3　としたとき、(直感的に)以下のように分割するのがよい

　　　　　　　　　　　　　↓

　　　　　　　　　　　　　↓

　　　　　　　　　　　　　↓

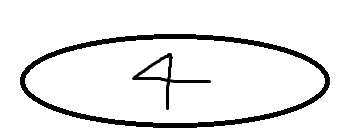
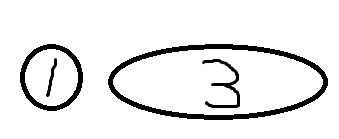
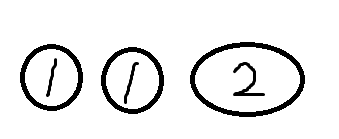
エスパーなので証明は考えない。

ソース

メモ化再帰でやろうとしてたコードも残ってます

#include <vector>
#include <list>
#include <map>
#include <set>
#include <deque>
#include <stack>
#include <bitset>
#include <algorithm>
#include <functional>
#include <numeric>
#include <utility>
#include <sstream>
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cctype>
#include <string>
#include <cstring>
#include <ctime>
#include <fstream>
#include <queue>
#include <complex>

using namespace std;

#define INF 1145141919
#define EPS 1e-9
#define PI acos(-1)
#define LL long long

LL gcd(LL a, LL b){ return (b) ? gcd(b, a%b) : a; }
LL lcm(LL a, LL b){ return (a*b) / gcd(max(a, b), min(a, b)); }

#define MAX_S 1001
#define MAX_TURN 1001

class SubdividedSlimes {
public:

	int memo[MAX_S][MAX_TURN];

	SubdividedSlimes(){
	
		memset(memo, -1, sizeof(memo));
	
	}

	int solve(int S, int turn){
	
		turn = min(S - 1, turn);

		cerr << S << " " << turn << endl;

		if (memo[S][turn] >= 0)
			return memo[S][turn];

		if (turn <= 0)
			return memo[S][turn] = 0;

		if (S == 1)
			return memo[S][turn] = 0;

		int ret = 0;

		for (int a = S / 2; a >= 1; a--){
		
			int b = S - a;

			int nextTurn = turn - 1;
			for (int i = 0; i <= nextTurn; i++){
				ret = max(ret, solve(a, i) + solve(b, nextTurn - i) + a*b);
			}
		
		}

		//cerr << S << " " << turn << " " << ret << endl;

		return memo[S][turn] = ret;
	
	}

	bool check(int S, int M, int cut){
	
		int num = S / (cut + 1);
		int numPlus = S % (cut + 1);

		int ans = 0;

		int a = num;
		if (numPlus > 0){
			a++;
			numPlus--;
		}

		while (cut > 0){
		
			cut--;

			int b = num;
			if (numPlus > 0){
				numPlus--;
				b++;
			}

			ans += a*b;
			a += b;
		
		}

		return ans >= M;
	
	}

	int needCut(int S, int M) {
		
		/*

		int left = 0, right = S+1;

		while (right - left > 1){
		
			int mid = (left + right) / 2;
			//cerr << mid << " " << solve(S, mid) << endl;
			if (solve(S, mid) >= M){
				right = mid;
			}
			else{
				left = mid;
			}
		
		}

		if (right >= S)
			return -1;
		else
			return right;

		*/

		for (int cut = 1; cut < S; cut++){
		
			if (check(S, M, cut))
				return cut;
		
		}

		return -1;

	}
};